
一、二叉树的查找
1.二叉查找树
对于树结构的查找,因为实际运用中大多都是使用二叉树的结构,因此我们只讨论二叉树的查找。
若有一棵非空二叉树,他满足如下条件:
- 若他的左子树不为空树,则有左子树上所有结点的值小于根结点的值。
- 若他的右子树不为空树,则有右子树上所有节点的值大于根结点的值。
- 他的左右子树也满足上述两个条件。
- 不能有值相等的结点。
则称这棵树为二叉查找/排序/搜素树。对二叉查找树进行中序遍历可以获取一个有序(升序)排列的集合。

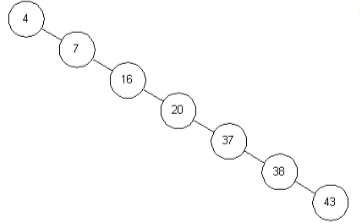
若对一棵普通的二叉查找树查找操作,则过程与二分查找类似,且查找的次数不会超过树的高度。此时查找到额时间复杂度为O(log2n);但若是出现极端情况,一棵二叉查找树完全没有左孩子或完全没有右孩子,此时变成链表结构,查找的时间复杂度也随之变成O(n)。因此,为了提升查询效率,在构建查找树时要尽可能的保证左右子树的结点数量相近,以保证查找效率。
二叉查找树的简单实现:
/*** 二叉查找功能接口* Created by bzhang on 2019/3/2.*/public interface TreeList { //获取根结点 Node getRoot(); // 返回树中的结点数,即数据元素的个数。 int size(); //树的高度 int getHeight(); // 返回树中排在 key 的数据元素 Object get(int key); //向树中增加结点 void put(int key,Object value); // 如果树为空返回 true,否则返回 false。 boolean isEmpty(); // 判断树中是否包含数据元素 e boolean contains(int key); //删除树中排在key位置的结点 boolean remove(int key); //中序遍历 void inOrder();} 接口实现类:
/*** 底层为链表实现的二叉查找树的实现。* Created by bzhang on 2019/3/2.*/public class TreeListImpl implements TreeList { private int size; //树中的结点数 private Node root; //跟结点 @Override public Node getRoot() { return root; } @Override public int size() { return size; } @Override public int getHeight() { return getHeight(root); } //实际计算二叉树高度的方法 private int getHeight(Node node) { if (node==null){ return 0; }else { int r = getHeight(node.getRight()); int l = getHeight(node.getLeft()); return r>l?(r+1):(l+1); } } @Override public Object get(int key) { Node temp = root; while (temp!=null){ //当前结点不为空,进入循环 if (temp.getKey()==key){ //key与结点的key相等,则返回结点的value值。 return temp.getValue(); }else if(temp.getKey()>key){ //key小于当前结点的key值,去查找当前节点的左子树 temp = temp.getLeft(); }else if (temp.getKey() key){ //key小于当前结点的key值,往其左子树中增加结点 res = temp; temp = temp.getLeft(); }else if (temp.getKey() key){ //判断新建结点是res左孩子还是右孩子 res.setLeft(newNode); }else { res.setRight(newNode); } size++; } @Override public boolean isEmpty() { return size == 0; } @Override public boolean contains(int key) { Node temp = root; while (temp!=null){ if (temp.getKey()==key){ return true; }else if(temp.getKey()>key){ temp = temp.getLeft(); }else if (temp.getKey() key){ temp = temp.getLeft(); }else if (temp.getKey() stack = new LinkedList(); Node temp = root; while (temp!=null||!stack.isEmpty()){ while (temp!=null){ stack.push(temp); temp = temp.getLeft(); } if (!stack.isEmpty()){ temp = stack.pop(); System.out.print("key:"+temp.getKey()+"*value:"+temp.getValue()+"||"); temp = temp.getRight(); } } System.out.println(""); } //判断是否为空树 private void checkedNotNull(Node root) { if (root==null){ throw new RuntimeException("空树不能进行遍历"); } }} 2.平衡二叉树
在二叉查找树中有个很打的缺陷:可能出现二叉查找树变为链表,即时间复杂度向O(n)倾斜。为了解决该问题,我们需要在向树中添加元素时做到自动平衡功能,即要让树保持:树中任意结点的左右子树的高度差(平衡因子)不能大于1。满足这个条件的二叉查找树,称之为平衡二叉树。
- 平衡因子:又称平衡度,表示的是结点的左右子树的差值。
建立平衡二叉树的目的为了减少二叉查找树的查找次数。我们知道,在二叉查找树中查找某个元素的次数与二叉查找树的高度有着:n<=high的关系(其中,n为查找次数,high为高度)。因此,减少二叉树的高度(层次),便能有效的提高查找的速度。
常见的实现二叉查找树自平衡的算法有:AVL树,红黑树,替罪羊树等。另外还有不是二叉树的平衡树,B树,B+树等(不做过多讨论)。因为Java中HashMap、TreeSet和TreeMap底层采用红黑树,这里只讨论红黑树。